The resolution of a microscope objective is defined as the smallest distance between two points on a specimen that can still be distinguished as two separate entities. Resolution is a somewhat subjective value in microscopy because at high
magnification, an image may appear unsharp but still be resolved to the maximum ability of the objective. Numerical aperture determines the resolving power of an objective, but the total resolution of a microscope system is also dependent upon the numerical aperture of the substage condenser. The higher the numerical aperture of the total system, the better the resolution.

The numerical aperture (N.A.) is basically a value that describes the quality of a lens. It is derived from the size of the lens, its working distance and the index of refraction. All quality objective lens will state the numerical aperture on the side of the barrel. A good rule of thumb is that the effective magnification of an objective is its numerical aperture times 1000. So a 40 x objective that has a N.A. of 0.65 has an effective magnification of 650 times. If you magnify beyond this you will only get empty magnification. You can calculate the theoretical resolution of any optical system using Abbe's equation. To calculate the resolution of the objective above multiple the wavelength of green light(0.5 micrometers) times the constant .61 divided by the N.A. The result will be 0.47 micrometers. In another example you can calculate the resolution of a pair of 8 x 20 binoculars. The number 8 is the magnification and the number 20 is the diameter of the objective lens. Assume you were looking at a specimen 100 ft away the alpha would be 0.0188 degrees. Plugging in abbe's equation the result for red light (650 nm) is 1.2 mm. Remember, this is a theoretical value with is the best possible resolution possible. The practical resolution will always be less due to optical aberratio.
 

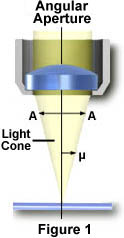
The angle m is one-half the angular aperture (A) and is related to  the numerical aperture through the following equation:

                         Numerical Aperture (NA) = n(sin m)

  where n is the refractive index of the imaging medium between  the front lens of the objective and the specimen cover glass, a  value that ranges from 1.00 for air to 1.51 for specialized  immersion oils. From this equation it is obvious that when the  imaging medium is air (with a refractive index, n = 1.0), then the numerical aperture is dependent only upon the angle m whose  maximum value is 90°. The sin of the angle m, therefore, has a  maximum value of 1.0 (sin(90°) = 1), which is the theoretical maximum numerical aperture of a lens operating with air as the imaging medium (using "dry" microscope objectives).
 

An important concept to understand in image formation is the nature of diffracted light rays intercepted by the objective. Only in cases where the higher (1st, 2nd, 3rd, etc.) orders of diffracted rays are captured, can interference work to recreate the image in the intermediate image plane of the objective. When only the zeroth order rays are captured, it is virtually impossible to reconstitute a recognizable image of the specimen. When 1st order light rays are added to the zeroth order rays, the image becomes more coherent, but it is still lacking in sufficient detail. It is only when higher order rays are recombined, that the image will represent the true architecture of the specimen. 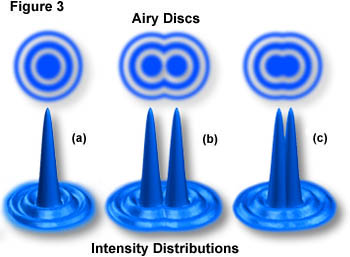This is the basis for the necessity of large numerical apertures (and subsequent smaller Airy disks) to achieve high-resolution images with an optical microscope.